Извлекаем корень
При численном решении задач по математике часто приходится выполнять операцию извлечения корня, то есть по числу s ≥ 0 находить такой x ≥ 0, что x2 = x · x = s. Это легко сделать на калькуляторе, но немногие умеют это делать вручную. Посмотрим, как это делается.
Как и при делении в столбик чисел, цифры ответа ищут по очереди слева направо. Кроме таблицы умножения для цифр (целых чисел, не больших 9) и функции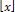 
целой части числа x, надо знать ещё формулу квадрата суммы – (a + b)2 = a2 + 2a · b + b2.
С её помощью легко возводить в квадрат, например:
Увеличив масштаб x на 1, мы число цифр его квадрата увеличиваем на 2: (10 · x)2 = 100 · x2.
Поэтому цифры числа под корнем разбивают справа на пары, например, числа s = 541962. Ища у корня сотни, берём только самую левую пару: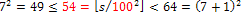 
.
Масштаб десятков: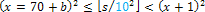 
. Гасим сотни: 54 – 72 = 5. Но 0 ≤ b2 ≤ 9b, и, беря вторую пару: 140b ≤ 519 < 141 + (140 + 11) · b, или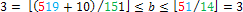 
Масштаб единиц: (x = 730 + c)2 ≤ s < (731 + c)2. Гасим десятки по формуле квадрата суммы – сотни уже погашены, вычтем 2a · b + b2: 519 – 2 · 7 · 3 · 10 – 32 = 90. Но 0 ≤ c2 ≤ 9c, и, беря третью пару: 1460c ≤ 9062 < 1461 + (1460 + 1) · c, или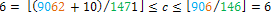 
.
Гасим единицы: 9062 – 2 · 73 · 6 · 10 – 62 = 266 > 0, значит, у корня есть и дробная часть.
Быстрее работает метод Ньютона: взяв x0 близко к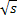 
, вычислим 
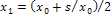, и т.д. 
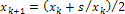, тогда 
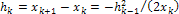, на каждом шаге число точных знаков примерно удваивается.
