Образовательный портал Математика для всех

Джузеппе Пеано

27.08.1858 – 20.04.1932

Итальянский математик. Внёс вклад в математическую логику, аксиоматику и философию математики, создал искусственный язык латино-сине-флексионе, обобщил понятие производной и оценил ряд Тейлора. Автор стандартной аксиоматизации натуральной арифметики — арифметики Пеано.

В 1860-х Грассман заметил, что многие факты арифметики можно вывести из простых свойств функции следования и математической индукции. Пирс в 1881 дал аксиомы арифметики натуральных чисел. Развивая идеи Грассмана, Пеано в 1889 формально определил сами натуральные числа.

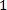1. является натуральным числом.
2. За каждым натуральным числом непосредственно следует ровно одно натуральное число .
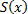3. Для каждого натурального числа 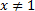существует единственное натуральное число 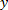, такое, что .
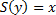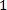4. не следует ни за каким натуральным числом.
5. (Аксиома индукции.) Если какое-либо предложение доказано для 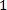, и из допущения, что оно верно для натурального числа , вытекает, что оно верно для 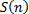, то это предложение верно для всех натуральных чисел.

За год до Пеано подобную систему аксиом опубликовал Дедекинд. Непротиворечивость арифметики Пеано в 1936 доказал Генцен с помощью трансфинитной индукции. Из теорем Гёделя следует, что доказательство нельзя провести средствами самой арифметики Пеано, и что существуют утверждения о натуральных числах, которые из аксиом Пеано нельзя ни вывести, ни опровергнуть.

Формализация арифметики включает в себя аксиомы Пеано, число 0 и операции сложения и умножения с аксиомами:

1. ;
2. ;
3. ;
4. .

А для ряда Тейлора его остаточный член позволил доказывать теоремы:

где – непрерывная в точке функция, и .

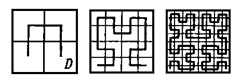В 1890 он первым построил непрерывную жорданову кривую, целиком заполняющую квадрат. Более поздний пример Гильберта является фракталом с размерностью Хаусдорфа .